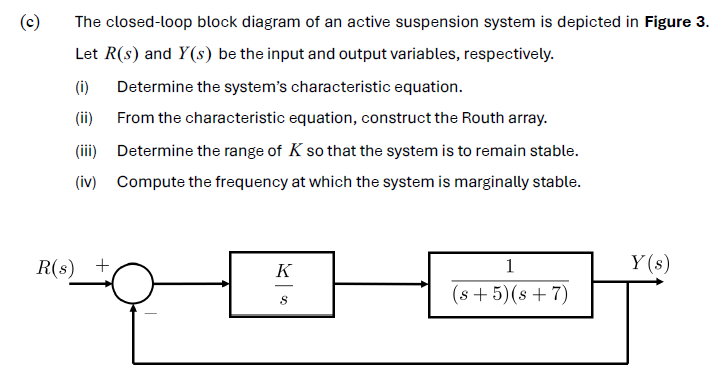
(c) The closed-loop block diagram of an active suspension system is depicted in Figure 3. Let R(s) and Y(s) be the input and output variables, respectively. (i) Determine the system's characteristic equation. (ii) From the characteristic equation, construct the Routh array. (iii) Determine the range of K so that the system is to remain stable. (iv) Compute the frequency at which the system is marginally stable.
![Imaging with a Thick Lens. Consider a glass lens of refractive index n , the z axis and thickness d , and two spherical surfaces of equal radii R as shown in Figure 3.1. Determine the ray-transfer matrix of the system between the two planes at distances d 1 and d 2 from the vertices of the lens. The lens is placed in air ( n = 1 ) . Show that the system is an imaging system (i.e., the input and output planes are conjugate) if 1 z 1 + 1 z 2 = 1 f or s 1 s 2 = f 2 , where z 1 = d 1 + h s 1 = z 1 − f z 2 = d 2 + h s 2 = z 2 − f and h = ( n − 1 ) f d n R 1 f = n − 1 R [ 2 − n − 1 n d R ] The points F 1 and F 2 are known as the front and back focal points, respectively. The points P 1 and P 2 are known as the first and second principal points, respectively. Show the importance of these points by tracing the trajectories of rays that are incident parallel to the optical axis. Figure 3.1: Imaging with a thick lens. P 1 and P 2 are the principal points and F 1 and F 2 are the focal points. Imaging with a Thick Lens. Consider a glass lens of refractive index n , the z axis and thickness d , and two spherical surfaces of equal radii R as shown in Figure 3.1. Determine the ray-transfer matrix of the system between the two planes at distances d 1 and d 2 from the vertices of the lens. The lens is placed in air ( n = 1 ) . Show that the system is an imaging system (i.e., the input and output planes are conjugate) if 1 z 1 + 1 z 2 = 1 f or s 1 s 2 = f 2 , where z 1 = d 1 + h s 1 = z 1 − f z 2 = d 2 + h s 2 = z 2 − f and h = ( n − 1 ) f d n R 1 f = n − 1 R [ 2 − n − 1 n d R ] The points F 1 and F 2 are known as the front and back focal points, respectively. The points P 1 and P 2 are known as the first and second principal points, respectively. Show the importance of these points by tracing the trajectories of rays that are incident parallel to the optical axis. Figure 3.1: Imaging with a thick lens. P 1 and P 2 are the principal points and F 1 and F 2 are the focal points.](https://www.doubtrix.com/uploads/editor/9885508202VQeDlDyKSs.png)
