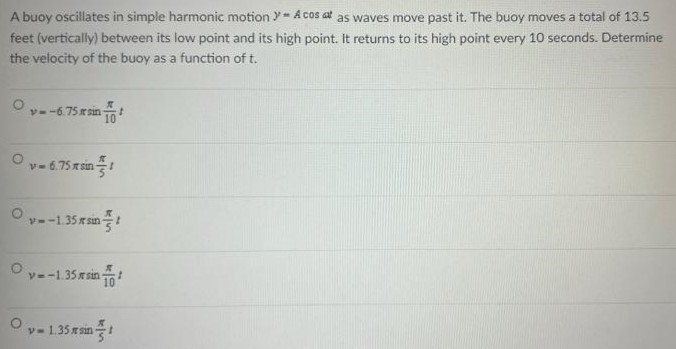
A buoy oscillates in simple harmonic motion y = Acosωt as waves move past it. The buoy moves a total of 13.5 feet (vertically) between its low point and its high point. It returns to its high point every 10 seconds. Determine the velocity of the buoy as a function of t. v = −6.75πsinπ 10t v = 6.75πsinπ 5t v = −1.35πsinπ5 t v = −1.35πsinπ10 v = 1.35πsinπ5 t