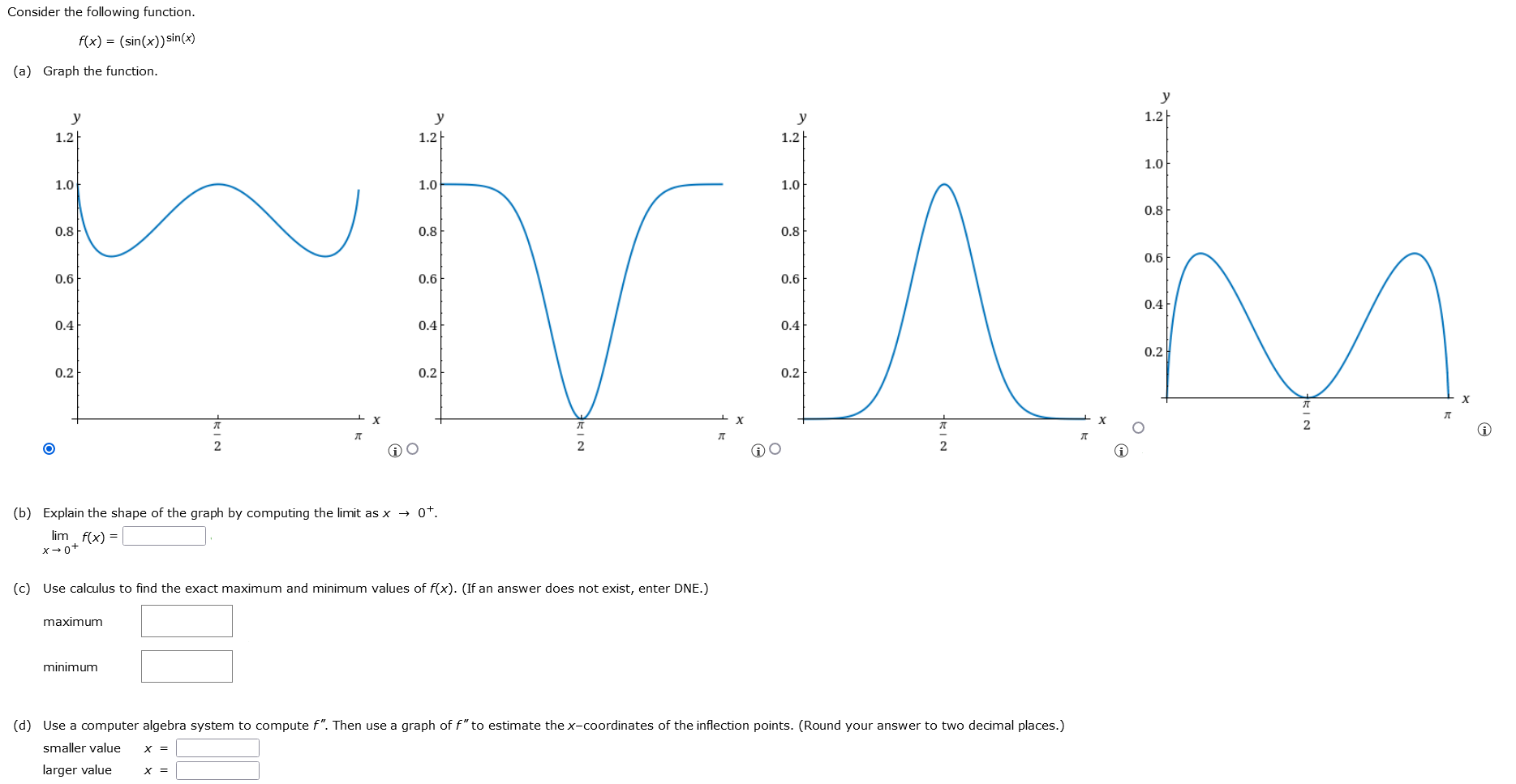
Consider the following function. f(x) = (sin(x))sin(x) (a) Graph the function. (b) Explain the shape of the graph by computing the limit as x→0+. limx→0+ f(x) = (c) Use calculus to find the exact maximum and minimum values of f(x). (If an answer does not exist, enter DNE.) (d) Use a computer algebra system to compute f′′. Then use a graph of f′′ to estimate the x-coordinates of the inflection points. (Round your answer to two decimal places.) smaller value x = larger value x =