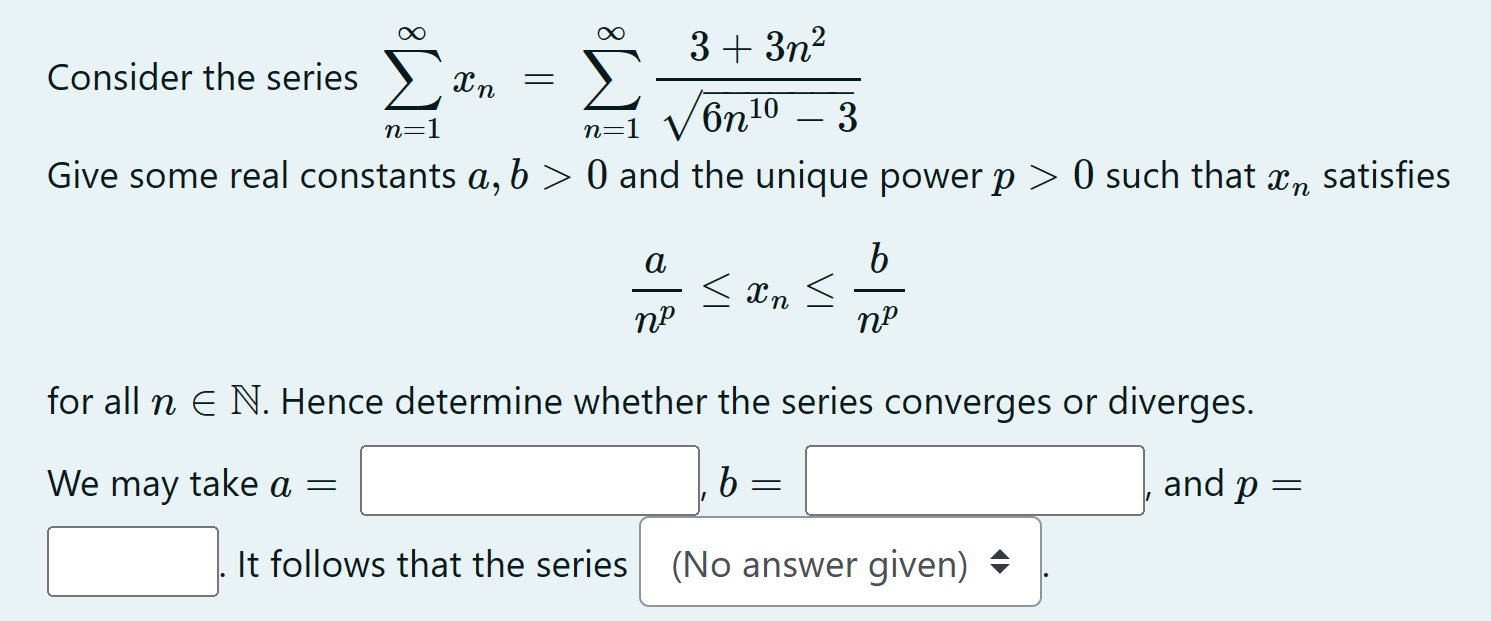
Consider the series ∑n = 1∞xn = ∑n = 1∞3+3 n26 n10−3 Give some real constants a, b > 0 and the unique power p > 0 such that xn satisfies anp ≤ xn ≤ bnp for all n∈N. Hence determine whether the series converges or diverges. We may take a = , b = and p = It follows that the series (No answer given)