Determine a region of the xy-plane for which the given differential equation would have a unique solution whose graph passes through a point (x0,y0) in the region. (4-y^2)y' = x^2 (1) A unique solution exists in the regions y < -2,-2 < y < 2,and y > 2. (2) A unique solution exists in the entire xy-plane. (3) A unique solution exists in the region y < 2. (4) A unique solution exists in the region y >
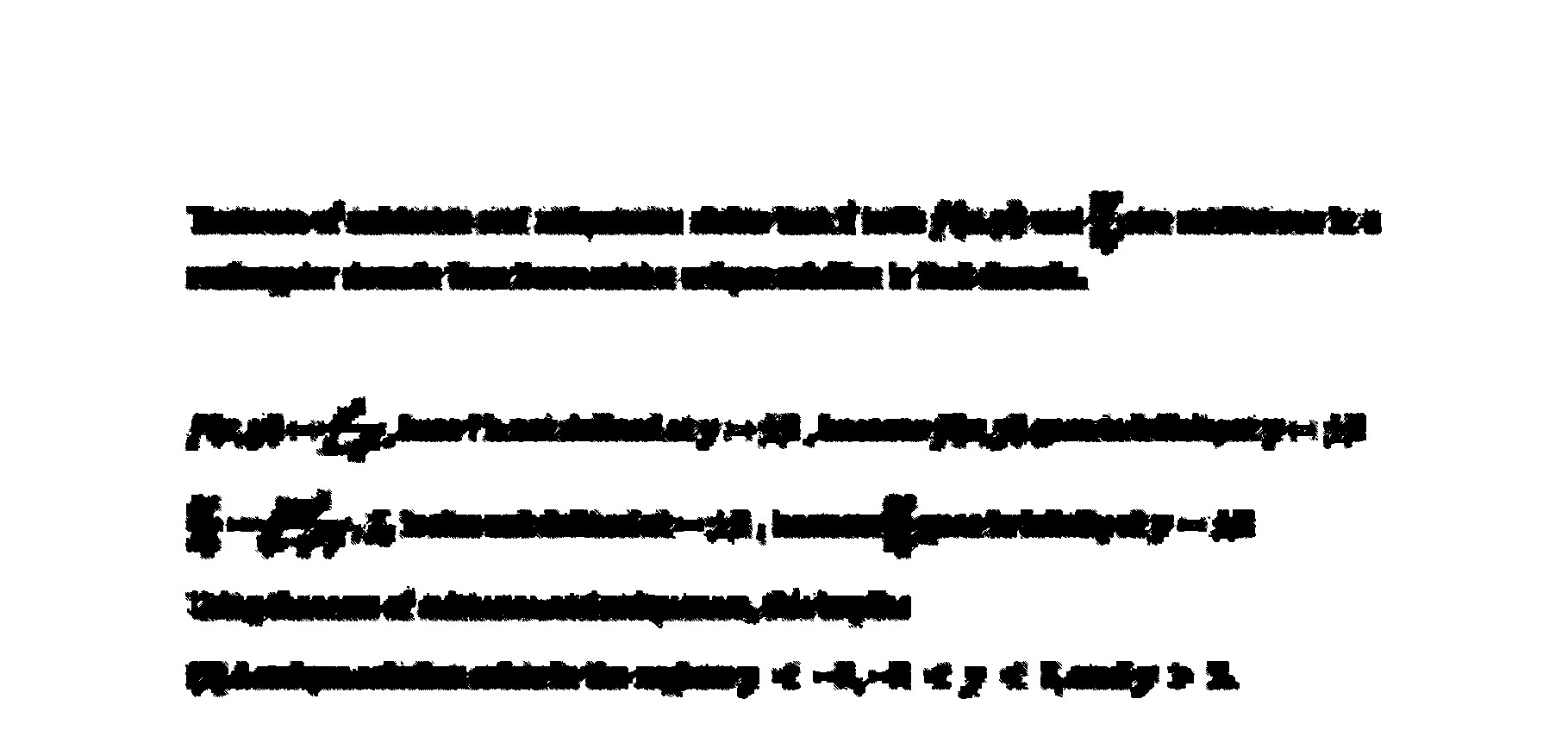

You'll get a detailed, step-by-step and expert verified solution.
 Work With Experts to Reach at Correct Answers
Work With Experts to Reach at Correct Answers