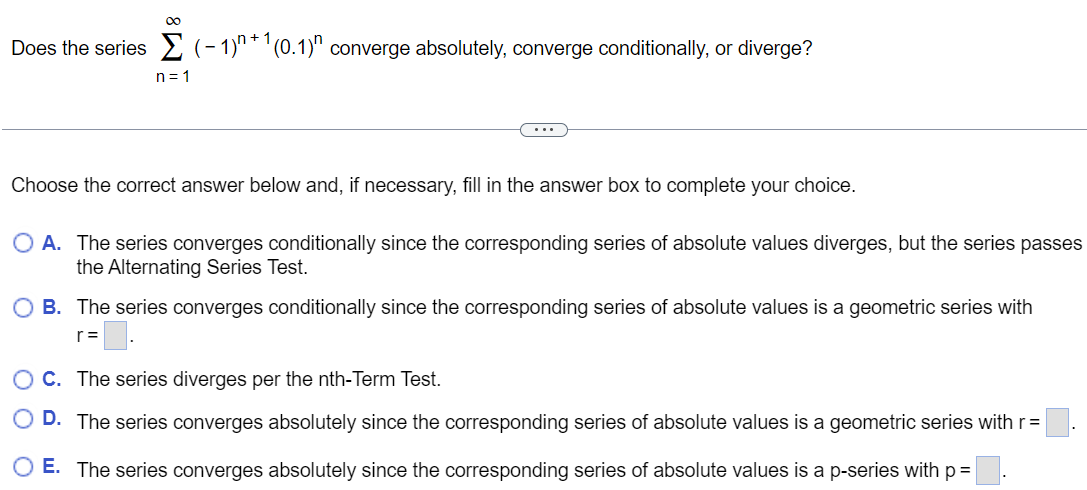
Does the series ∑n = 1∞(−1)n+1(0.1)n converge absolutely, converge conditionally, or diverge? Choose the correct answer below and, if necessary, fill in the answer box to complete your choice. A. The series converges conditionally since the corresponding series of absolute values diverges, but the series passes the Alternating Series Test. B. The series converges conditionally since the corresponding series of absolute values is a geometric series with r = . C. The series diverges per the nth-Term Test. D. The series converges absolutely since the corresponding series of absolute values is a geometric series with r = E. The series converges absolutely since the corresponding series of absolute values is a p-series with p =