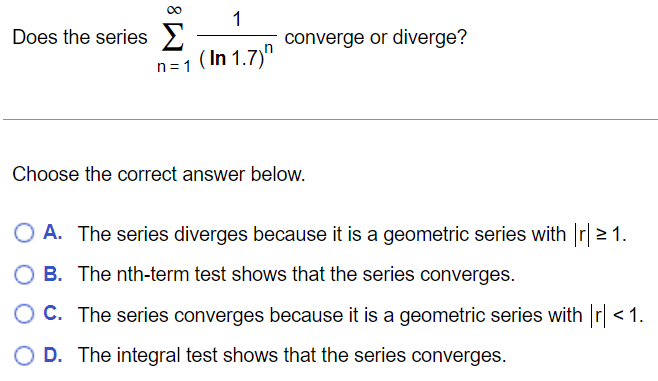Does the series ∑n = 1∞1(ln1.7)n converge or diverge? Choose the correct answer below. A. The series diverges because it is a geometric series with |r| ≥ 1. B. The nth-term test shows that the series converges. C. The series converges because it is a geometric series with |r| < 1. D. The integral test shows that the series converges.