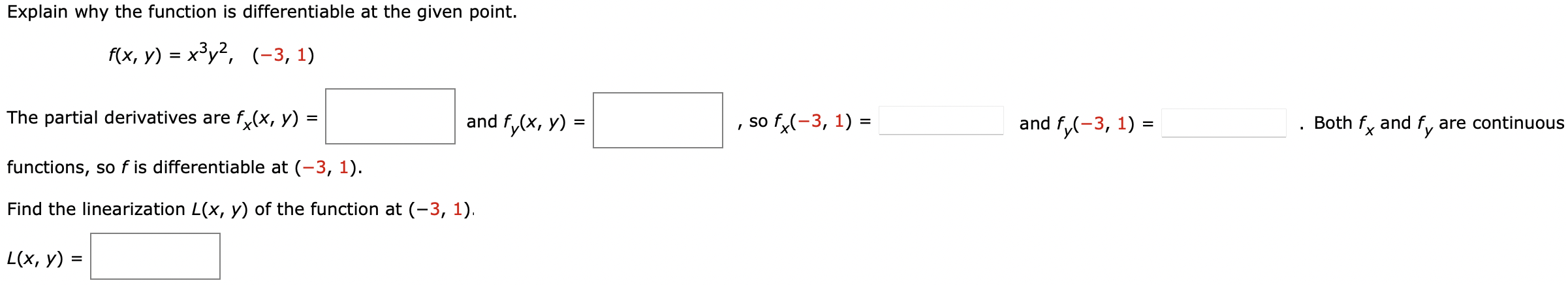Explain why the function is differentiable at the given point. f(x, y) = x3y2, (−3, 1) The partial derivatives are fx(x, y) = and fy(x, y) = , so fx(−3, 1) = and fy(−3, 1) = . Both fx and fy are continuous functions, so f is differentiable at (−3, 1). Find the linearization L(x, y) of the function at (−3, 1). L(x, y) =