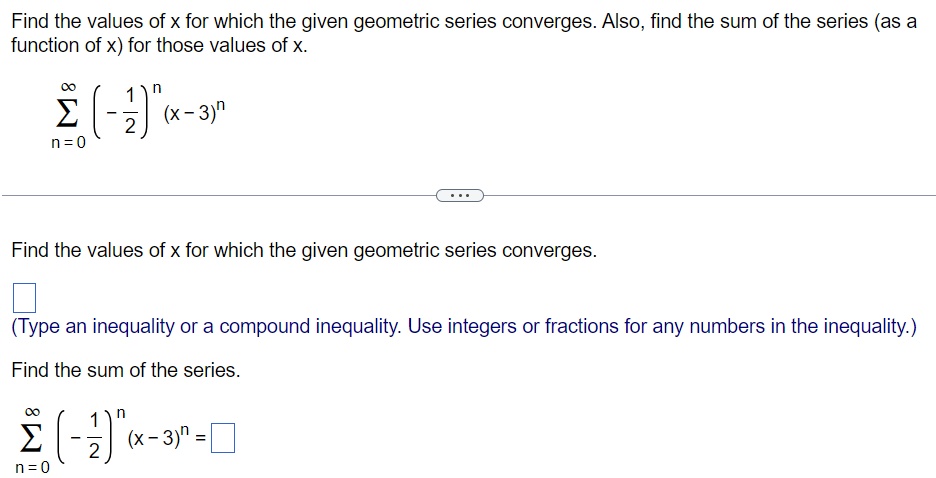
Find the values of x for which the given geometric series converges. Also, find the sum of the series (as a function of x) for those values of x. ∑n = 0∞(−12)n(x−3)n Find the values of x for which the given geometric series converges. (Type an inequality or a compound inequality. Use integers or fractions for any numbers in the inequality. ) Find the sum of the series. ∑n = 0∞(−12)n(x−3)n =