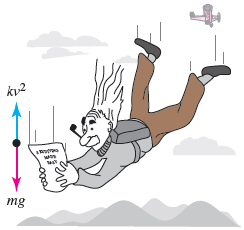
For high-speed motion through the air - such as a skydiver shown in the figure, falling before the parachute is opened - air resistance is close to a power of the instantaneous velocity v(t). Determine a differential equation for the velocity v(t) of a falling body of mass m if air resistance is proportional to the square of the instantaneous velocity. Assume the downward direction is positive. (Use k > 0 for the constant of proportionality, g > 0 for acceleration due to gravity, and v for v(t).) dv/dt



You'll get a detailed, step-by-step and expert verified solution.
 Work With Experts to Reach at Correct Answers
Work With Experts to Reach at Correct Answers