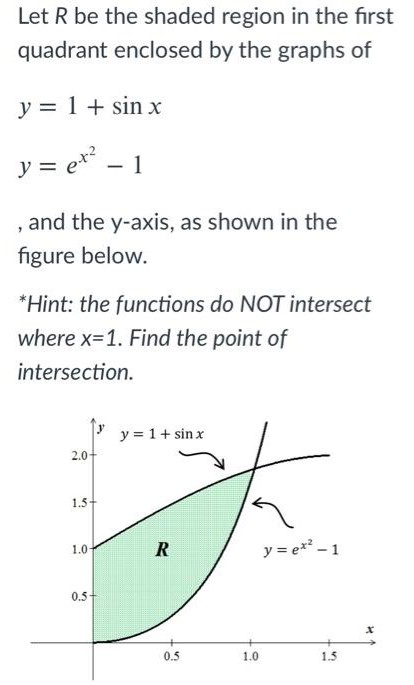
Let R be the shaded region in the first quadrant enclosed by the graphs of y = 1 + sinx y = ex2 − 1 , and the y-axis, as shown in the figure below. *Hint: the functions do NOT intersect where x = 1. Find the point of intersection. A) Find the area of the region R. B) Find the volume of the solid generated when the region R is revolved about the x-axis. C) The region R is the base of a solid. For this solid, each cross section perpendicular to the x-axis is a square. Find the volume of this solid.