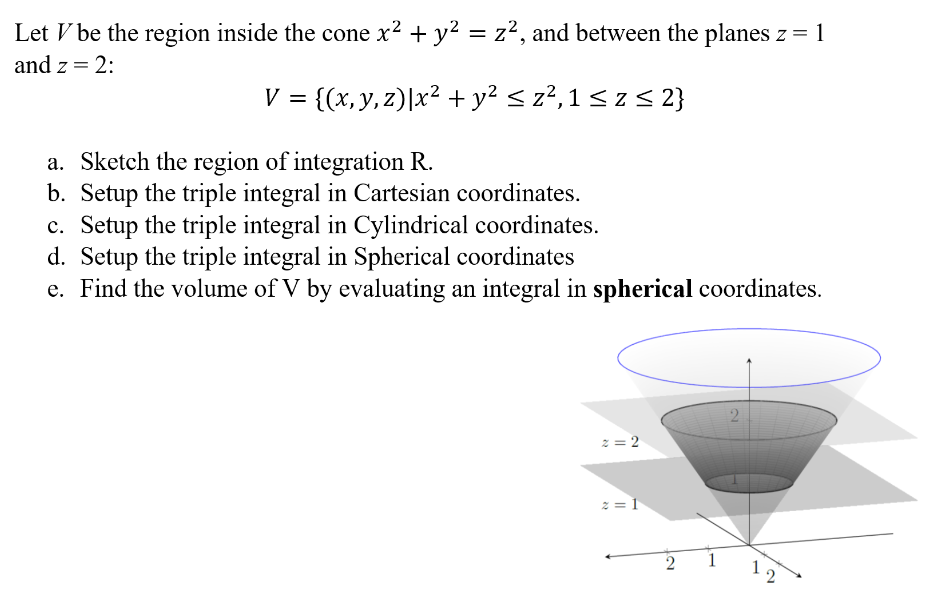
Let V be the region inside the cone x2+y2 = z2, and between the planes z = 1 and z = 2: V = {(x, y, z)∣x2 + y2 ≤ z2, 1 ≤ z ≤ 2} a. Sketch the region of integration R. b. Setup the triple integral in Cartesian coordinates. c. Setup the triple integral in Cylindrical coordinates. d. Setup the triple integral in Spherical coordinates e. Find the volume of V by evaluating an integral in spherical coordinates.