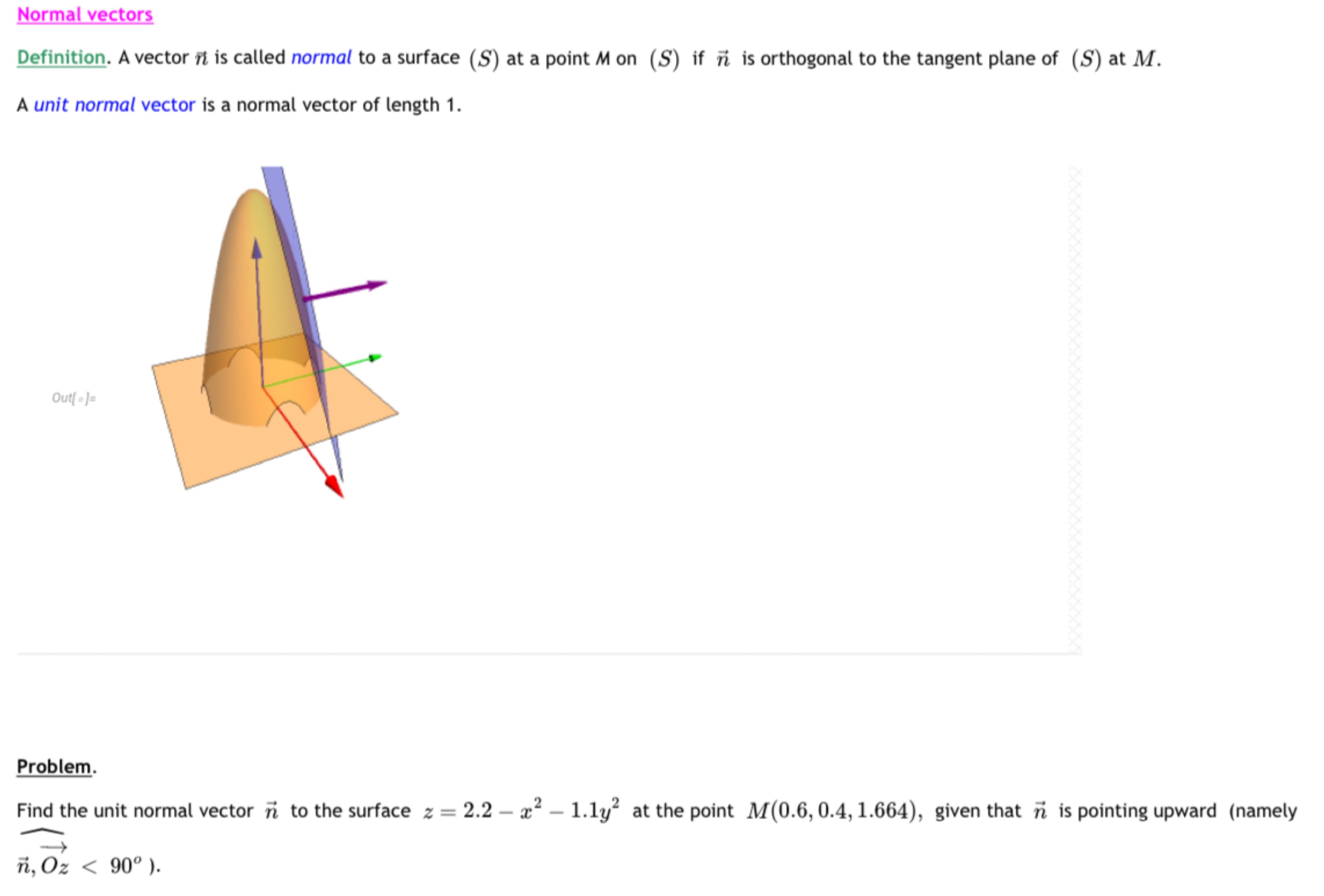
Normal vectors Definition. A vector n→ is called normal to a surface (S) at a point M on (S) if n→ is orthogonal to the tangent plane of (S) at M. A unit normal vector is a normal vector of length 1. Problem. Find the unit normal vector n→ to the surface z = 2.2 − x2 − 1.1y2 at the point M(0.6, 0.4, 1.664), given that n→ is pointing upward (namely n→, Oz→ < 90∘).