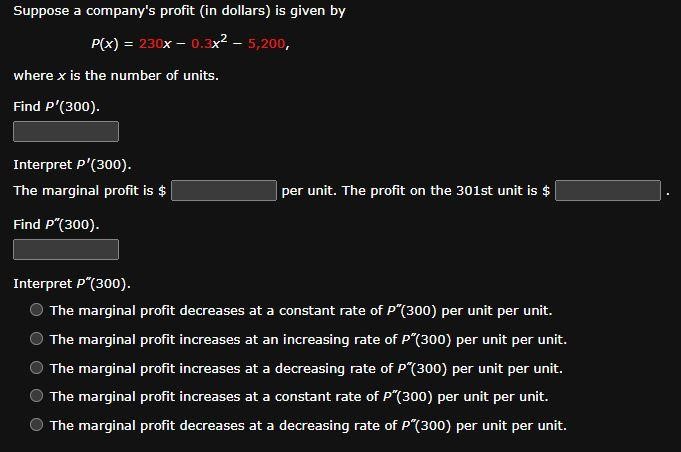
Suppose a company's profit (in dollars) is given by P(x) = 230x − 0.3x2 − 5,200, where x is the number of units. Find P′(300). Interpret P′(300). The marginal profit is $ per unit. The profit on the 301st unit is $ . Find P′′(300). Interpret P′′(300). The marginal profit decreases at a constant rate of P′′(300) per unit per unit. The marginal profit increases at an increasing rate of P′′(300) per unit per unit. The marginal profit increases at a decreasing rate of P′′(300) per unit per unit. The marginal profit increases at a constant rate of P′′(300) per unit per unit. The marginal profit decreases at a decreasing rate of P′′(300) per unit per unit.