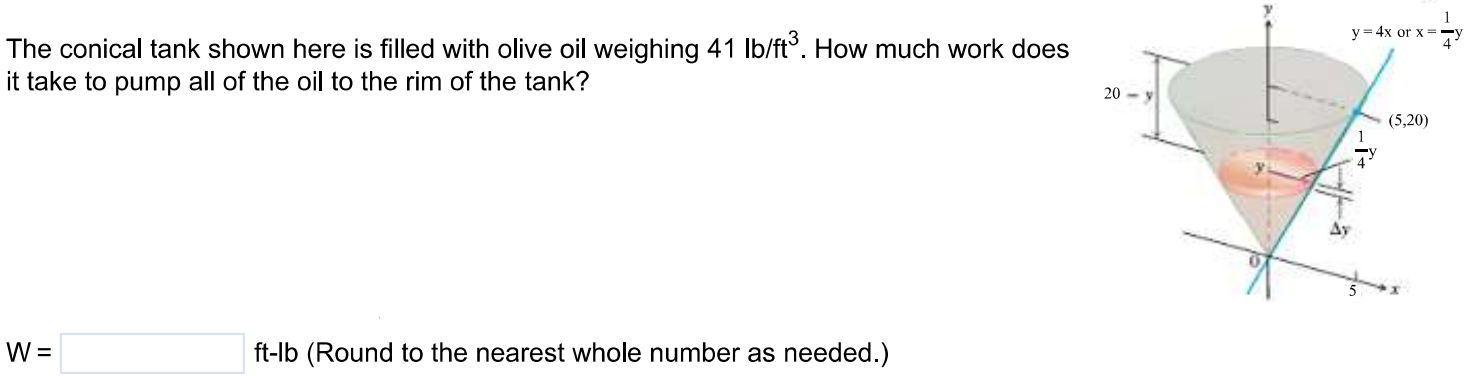
Step (1): First of all consider the oil is divided into different into thin slabs and a slab is situated at distance ‘y’ (from bottom of the cone) of thickness .

Step (2): Determine the volume of the considered oil slab using area and thickness of this slab.

Step (3): The force F(y) required to lift the considered oil slab using weight per unit volume and volume.

Step (4): The work required to lift the slab upto the rim of cone can be determined by multiplying force with distance.

Step (5): Since number of oil slabs ‘n’ tends to infinity, total work done can be calculated by integrating the work in the interval [0, 20].