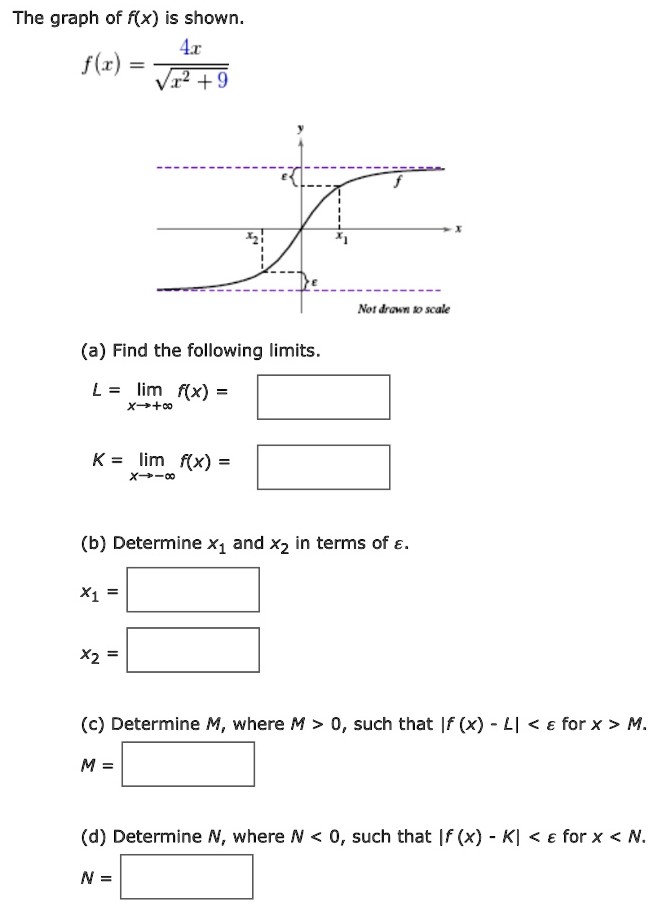
The graph of f(x) is shown. f(x) = 4x x2+9 (a) Find the following limits. L = limx→+∞ f(x) = K = limx→−∞ f(x) = (b) Determine x1 and x2 in terms of ε. x1 = x2 = (c) Determine M, where M > 0, such that |f(x)−L| < ε for x > M. M = (d) Determine N, where N < 0, such that |f(x)−K| < ε for x < N. N =