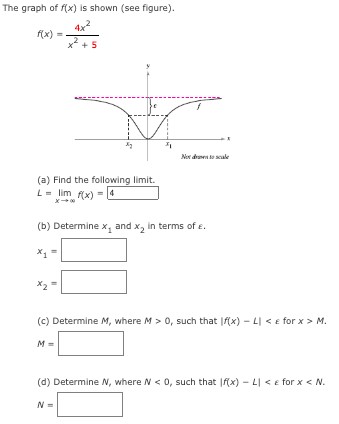
The graph of f(x) is shown (see figure). f(x) = 4 x2 x2+5 (a) Find the following limit. L = limx→∞ f(x) = (b) Determine x1 and x2 in terms of ε. x1 = x2 = (c) Determine M, where M > 0, such that |f(x)−L| < ε for x > M. M = (d) Determine N, where N < 0, such that |f(x)−L| < ε for x < N. N =
![CS Amplifiers vs. CG Amplifiers [19 points] (a) (b) Fig. P2 All NMOS transistors are biased at saturation region, but only small-signal equivalent circuits are shown in the figures. Each individual NMOS transistor has C2d = 0.1•Cgs, Cdb = Csb = 0.2•Cgs and intrinsic gain gmr0 = 40(>>1). However, the transistor is used as a CS amplifier in Fig. P2(a), but a CG amplifier in Fig. P2(b). Note that the intrinsic output impedance, r8, of the NMOS transistor still exists even though the value of Rsig and RL. have been assigned as rd/2 and re, respectively. For the following questions, please include device capacitances Cb, C2 d, Cb, and Cb if necessary. (a) Find the low frequency gain |vo/vi| of the CS amplifier in Fig. P2(a). (b) Use OCTC method only to find the expression of the time-constant, τ1,cs in terms of Cpd and ro, across the gate and source of the NMOS in Fig. P2(a). (c) Use OCTC method only to find the expression of the time-constant, τ22Cs in terms of Cpd and ro, across the drain and source of the NMOS in Fig. P2(a). (d) Use OCTC method only to find the expression of the time-constant, τ3, cs in terms of C84 and ro, across the drain and gate of the NMOS in Fig. P2(a). (e) Based on (b), (c), and (d), find the expression of 3-dB frequency, fucs in terms of Cp4 and rC, of the CS amplifier. (f) Find the low-frequency gain |v9/vi | of the CG amplifier in Fig. P2(b). (g) Use OCTC method only to find the expression of the time-constant, τ1,CG in terms of Cpd and r6, across the source and gate of the NMOS in Fig. P2(b). (h) Use OCTC method only to find the expression of the time-constant, τ2CG in terms of C84 and ro, across the drain and gate of the NMOS in Fig. P2(b). (i) Based on (g) and (h), find the expression of 3-dB frequency, f fh,co in terms of CBd and r0, of the CG amplifier. (j) Based on (a) and (f), find the ratio of low-frequency gains, |Av,co/Av, cs|. (k) Based on (c) and (i), find the ratio of 3-dB frequencies, fH,co/fH,cs. Result Summary: (a) Av,Cs = (b) τ1,Cs = (c) τ2,Cs = (d) τ3,Cs = (e) fH,CS = (f) Av,CG = (g) τ1,CG = (h) τ2,CG = (i) fH,CG = (j) |Av,CG/Av,CS| = (k) fH,CG/fH,CS =](https://www.doubtrix.com/uploads/editor/0923858882CLzEBqhtpd.jpg)
![CS Amplifiers vs. CG Amplifiers [19 points] (a) (b) Fig. P2 All NMOS transistors are biased at saturation region, but only small-signal equivalent circuits are shown in the figures. Each individual NMOS transistor has C2d = 0.1•Cgs, Cdb = Csb = 0.2•Cgs and intrinsic gain gmr0 = 40(>>1). However, the transistor is used as a CS amplifier in Fig. P2(a), but a CG amplifier in Fig. P2(b). Note that the intrinsic output impedance, r8, of the NMOS transistor still exists even though the value of Rsig and RL. have been assigned as rd/2 and re, respectively. For the following questions, please include device capacitances Cb, C2 d, Cb, and Cb if necessary. (a) Find the low frequency gain |vo/vi| of the CS amplifier in Fig. P2(a). (b) Use OCTC method only to find the expression of the time-constant, τ1,cs in terms of Cpd and ro, across the gate and source of the NMOS in Fig. P2(a). (c) Use OCTC method only to find the expression of the time-constant, τ22Cs in terms of Cpd and ro, across the drain and source of the NMOS in Fig. P2(a). (d) Use OCTC method only to find the expression of the time-constant, τ3, cs in terms of C84 and ro, across the drain and gate of the NMOS in Fig. P2(a). (e) Based on (b), (c), and (d), find the expression of 3-dB frequency, fucs in terms of Cp4 and rC, of the CS amplifier. (f) Find the low-frequency gain |v9/vi | of the CG amplifier in Fig. P2(b). (g) Use OCTC method only to find the expression of the time-constant, τ1,CG in terms of Cpd and r6, across the source and gate of the NMOS in Fig. P2(b). (h) Use OCTC method only to find the expression of the time-constant, τ2CG in terms of C84 and ro, across the drain and gate of the NMOS in Fig. P2(b). (i) Based on (g) and (h), find the expression of 3-dB frequency, f fh,co in terms of CBd and r0, of the CG amplifier. (j) Based on (a) and (f), find the ratio of low-frequency gains, |Av,co/Av, cs|. (k) Based on (c) and (i), find the ratio of 3-dB frequencies, fH,co/fH,cs. Result Summary: (a) Av,Cs = (b) τ1,Cs = (c) τ2,Cs = (d) τ3,Cs = (e) fH,CS = (f) Av,CG = (g) τ1,CG = (h) τ2,CG = (i) fH,CG = (j) |Av,CG/Av,CS| = (k) fH,CG/fH,CS =](https://www.doubtrix.com/uploads/editor/3268471942mKJBTBCcsa.jpg)
