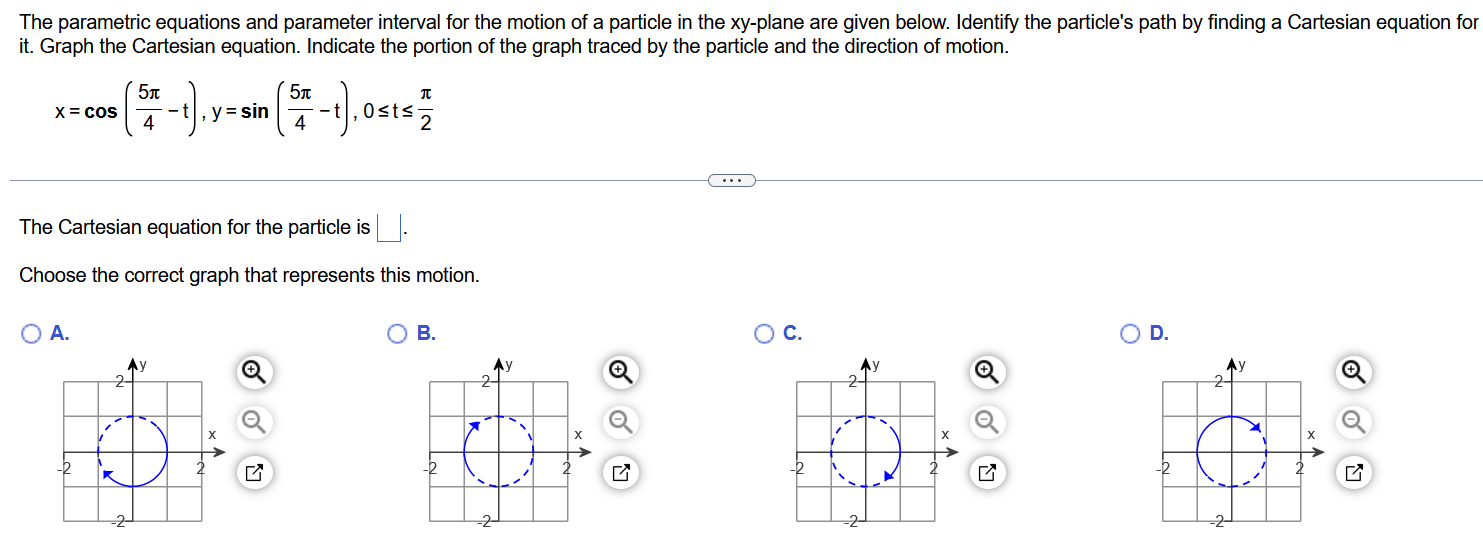
The parametric equations and parameter interval for the motion of a particle in the xy-plane are given below. Identify the particle's path by finding a Cartesian equation for it. Graph the Cartesian equation. Indicate the portion of the graph traced by the particle and the direction of motion. x = cos( 5π4 − t), y = sin( 5π4 − t),0≤ t ≤π2 The Cartesian equation for the particle is ◻ . Choose the correct graph that represents this motion. A. B. C. D.