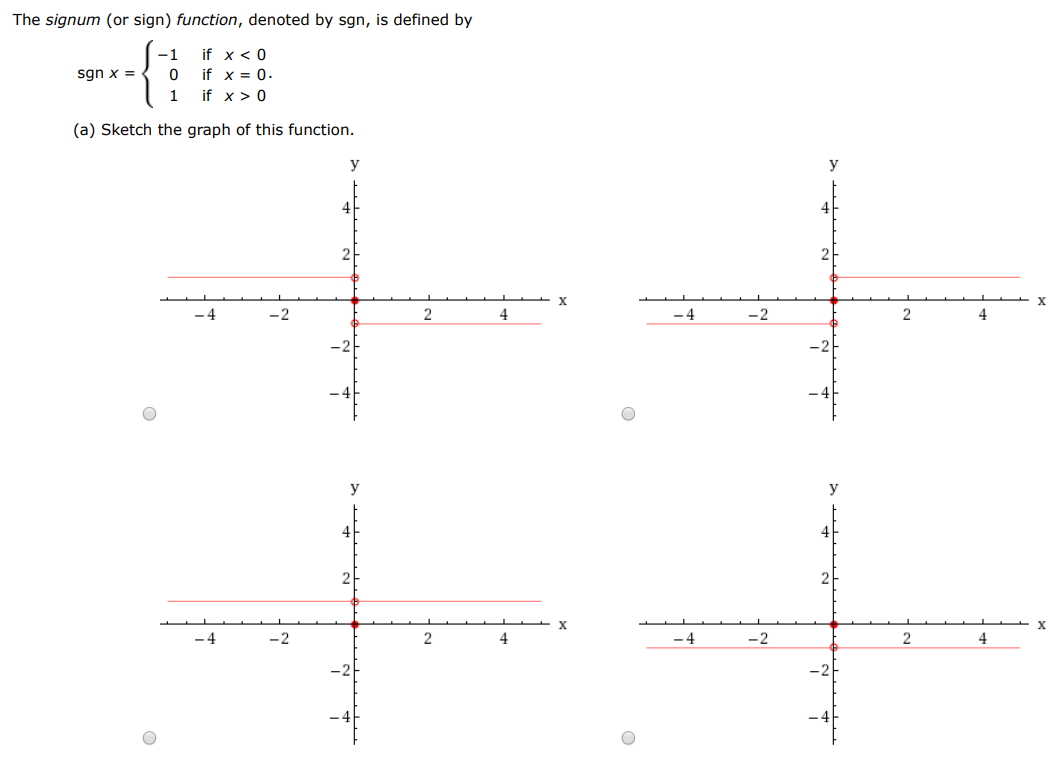
The signum (or sign) function, denoted by sgn, is defined by sgnx = {−1 if x < 0 0 if x = 0 1 if x > 0 (a) Sketch the graph of this function. (b) Find each of the following limits. (If an answer does not exist, enter DNE.) (i) limx→0+sgnx (ii) limx→0−sgnx (iii) limx→0 sgnx (iv) limx→0|sgnx|