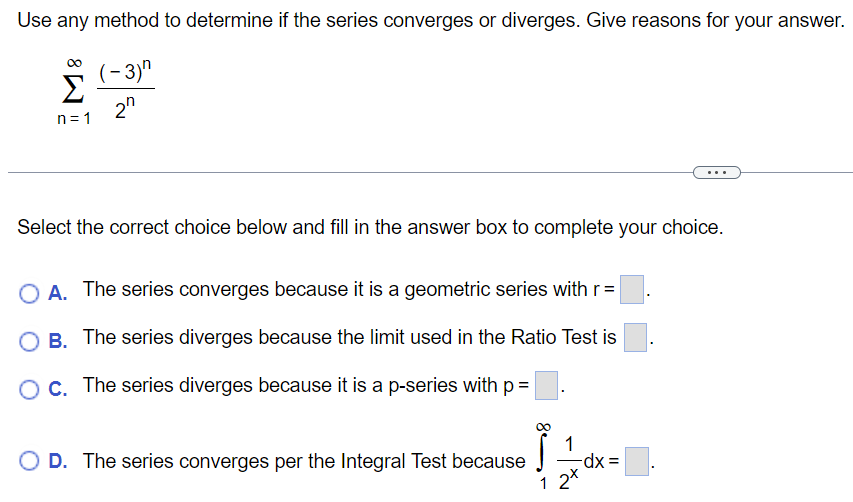
Use any method to determine if the series converges or diverges. Give reasons for your answer. ∑n = 1∞(−3)n2n Select the correct choice below and fill in the answer box to complete your choice. A. The series converges because it is a geometric series with r = . B. The series diverges because the limit used in the Ratio Test is C. The series diverges because it is a p-series with p = . D. The series converges per the Integral Test because ∫1∞12 xdx =