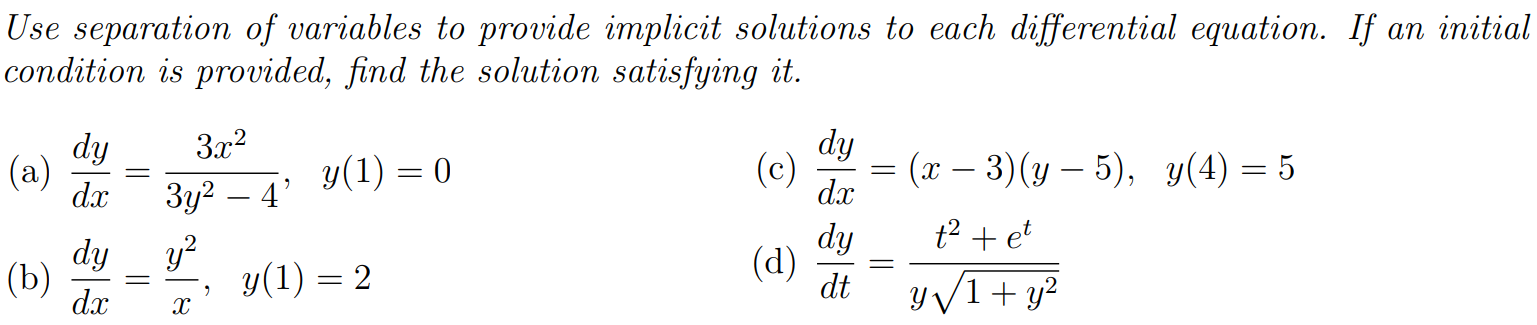Use separation of variables to provide implicit solutions to each differential equation. If an initial condition is provided, find the solution satisfying it. (a) dydx = 3x2 3y2−4, y(1) = 0 (c) dydx = (x−3)(y−5), y(4) = 5 (b) dydx = y2 x, y(1) = 2 (d) dydt = t2+et y1+y2