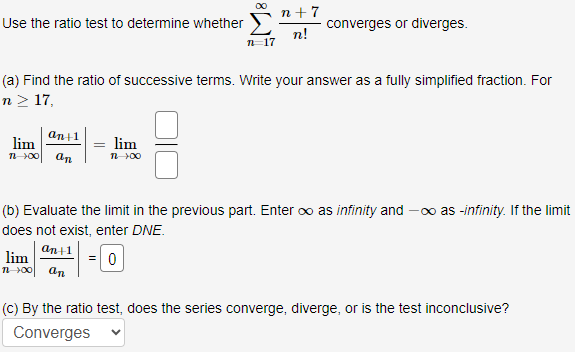
Use the ratio test to determine whether ∑n = 17∞n+7 n! converges or diverges. (a) Find the ratio of successive terms. Write your answer as a fully simplified fraction. For n ≥ 17, limn→∞|an+1 an| = limn→∞ (b) Evaluate the limit in the previous part. Enter ∞ as infinity and −∞ as -infinity. If the limit does not exist, enter DNE. limn→∞|an+1 an| = 0 (c) By the ratio test, does the series converge, diverge, or is the test inconclusive? Converges