What is the minimum value of n that will guarantee the estimate of the

Question

Notify Me Bookmark

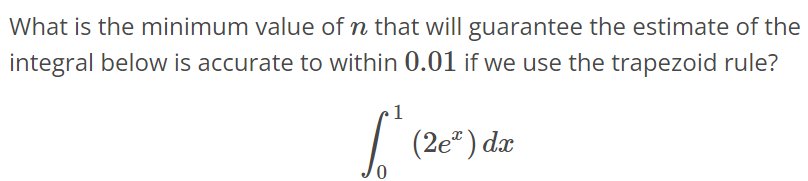
What is the minimum value of n that will guarantee the estimate of the integral below is accurate to within 0.01 if we use trapezoid rule? ∫ 1 0 (2e^x)dx

Image text

What is the minimum value of n that will guarantee the estimate of the integral below is accurate to within 0.01 if we use trapezoid rule? ∫ 1 0 (2e^x)dx

Explanation & Steps

We need to use error bound formula for the trapezoidal rule to determine the minimum value of n required such that the error in an area estimation of an integral by trapezoidal rule is less than a specified value.

Let f(x) be a continuous function over [a, b], having a second derivative f''(x) over this interval. If M is the maximum value of |f''(x)| over [a, b], then the upper bound for the error in using the trapezoidal rule, $T_n$ , to estimate $\int_{a}^{b}f(x)dx$ is: