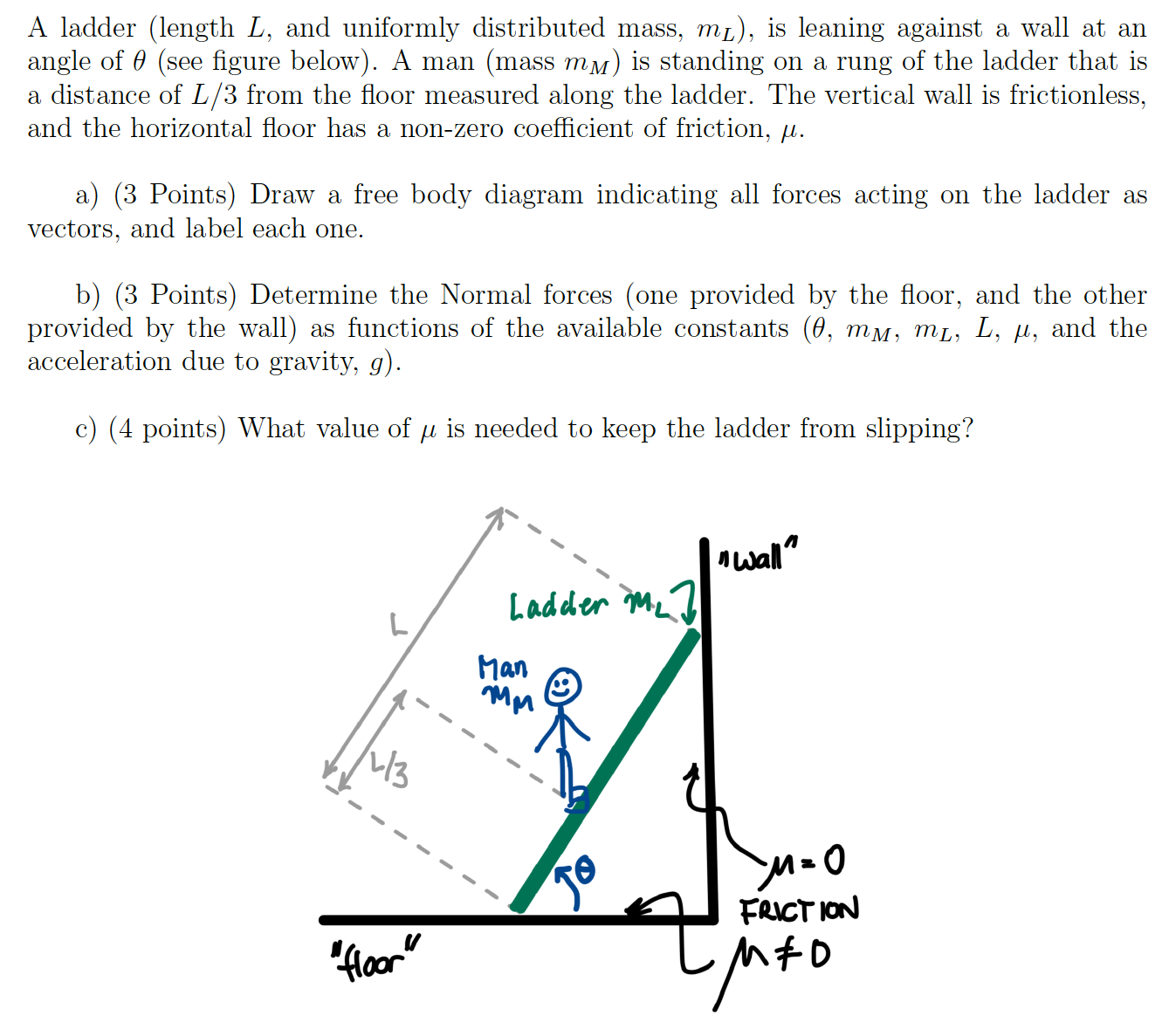
A ladder (length L, and uniformly distributed mass, mL), is leaning against a wall at an angle of θ (see figure below). A man (mass mM ) is standing on a rung of the ladder that is a distance of L/3 from the floor measured along the ladder. The vertical wall is frictionless, and the horizontal floor has a non-zero coefficient of friction, μ. a) (3 Points) Draw a free body diagram indicating all forces acting on the ladder as vectors, and label each one. b) (3 Points) Determine the Normal forces (one provided by the floor, and the other provided by the wall) as functions of the available constants (θ, mM, mL, L, μ, and the acceleration due to gravity, g). c) (4 points) What value of μ is needed to keep the ladder from slipping?