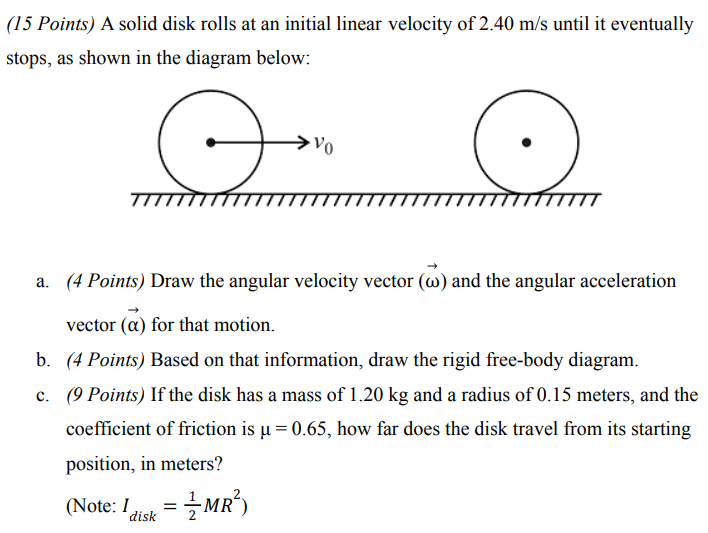
A solid disk rolls at an initial linear velocity of 2.40 m/s until it eventually stops, as shown in the diagram below: a. (4 Points) Draw the angular velocity vector (ω→) and the angular acceleration vector (α→) for that motion. b. (4 Points) Based on that information, draw the rigid free-body diagram. c. (9 Points) If the disk has a mass of 1.20 kg and a radius of 0.15 meters, and the coefficient of friction is μ = 0.65, how far does the disk travel from its starting position, in meters? (Note: Idisk = 12 MR2)