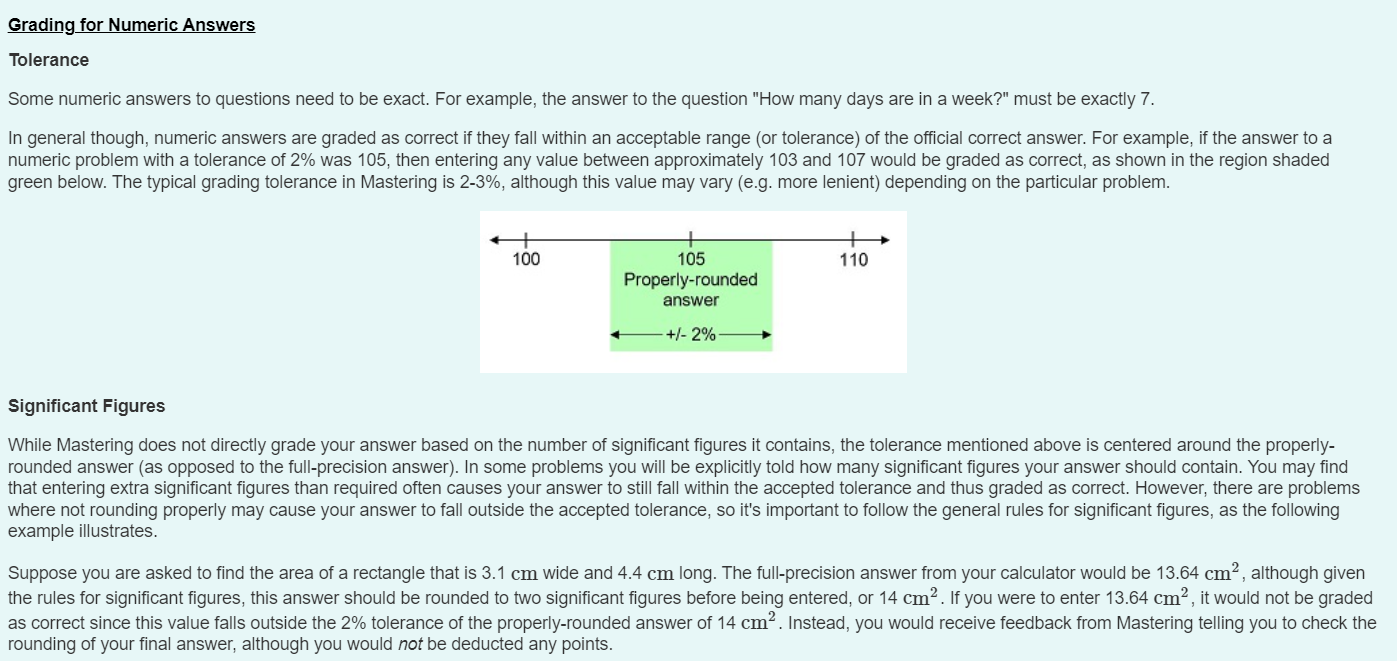
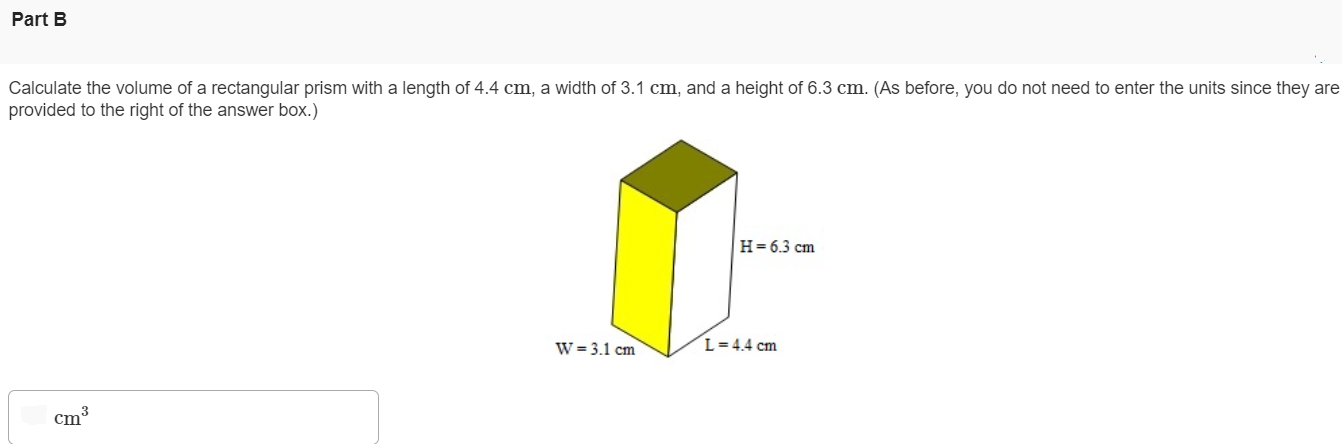
Grading for Numeric Answers Tolerance Some numeric answers to questions need to be exact. For example, the answer to the question "How many days are in a week?" must be exactly 7. In general though, numeric answers are graded as correct if they fall within an acceptable range (or tolerance) of the official correct answer. For example, if the answer to a numeric problem with a tolerance of 2% was 105, then entering any value between approximately 103 and 107 would be graded as correct, as shown in the region shaded green below. The typical grading tolerance in Mastering is 2-3%, although this value may vary (e.g. more lenient) depending on the particular problem. A number line is marked at 100, 105, and 110, where 105 is the properly-rounded answer. A green shaded region extends beyond 105 by 2 percent of this value in each direction. Significant Figures While Mastering does not directly grade your answer based on the number of significant figures it contains, the tolerance mentioned above is centered around the properly-rounded answer (as opposed to the full-precision answer). In some problems you will be explicitly told how many significant figures your answer should contain. You may find that entering extra significant figures than required often causes your answer to still fall within the accepted tolerance and thus graded as correct. However, there are problems where not rounding properly may cause your answer to fall outside the accepted tolerance, so it's important to follow the general rules for significant figures, as the following example illustrates. Suppose you are asked to find the area of a rectangle that is 3.1 cm wide and 4.4 cm long. The full-precision answer from your calculator would be 13.64 cm2, although given the rules for significant figures, this answer should be rounded to two significant figures before being entered, or 14 cm2. If you were to enter 13.64 cm2, it would not be graded as correct since this value falls outside the 2% tolerance of the properly-rounded answer of 14 cm2. Instead, you would receive feedback from Mastering telling you to check the rounding of your final answer, although you would not be deducted any points. Part A What is the area of a rectangle that is 3.1 cm wide and 4.4 cm long? Enter the full-precision answer first to see the corresponding feedback before entering the properly-rounded answer. (You do not need to enter the units in this case since they are provided to the right of the answer box). Part B Calculate the volume of a rectangular prism with a length of 4.4 cm, a width of 3.1 cm, and a height of 6.3 cm. (As before, you do not need to enter the units since they are provided to the right of the answer box.) Part C The momentum of an object is determined to be 7.2×10-3 kg⋅m/s. Express this quantity as provided or use any equivalent unit. (Note: 1 kg = 1000 g). Part D Enter the following expression in the answer box below: √2gλ3m, where λ is the lowercase Greek letter lambda.





You'll get a detailed, step-by-step and expert verified solution.
 Work With Experts to Reach at Correct Answers
Work With Experts to Reach at Correct Answers