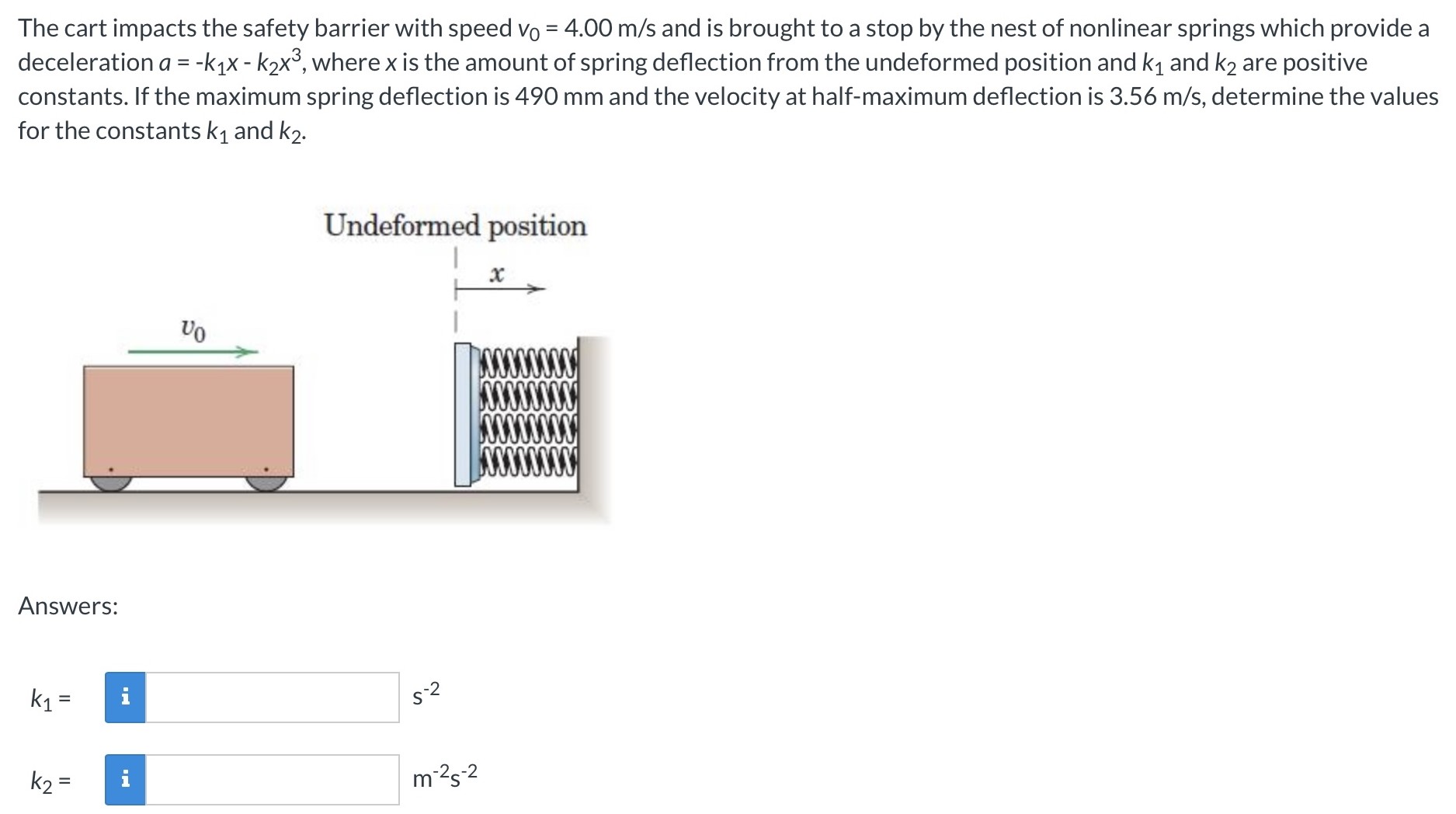
The cart impacts the safety barrier with speed v0 = 4.00 m/s and is brought to a stop by the nest of nonlinear springs which provide a deceleration a = −k1x − k2x3, where x is the amount of spring deflection from the undeformed position and k1 and k2 are positive constants. If the maximum spring deflection is 490 mm and the velocity at half-maximum deflection is 3.56 m/s, determine the values for the constants k1 and k2. Answers: k1 = s−2 k2 = m−2s−2