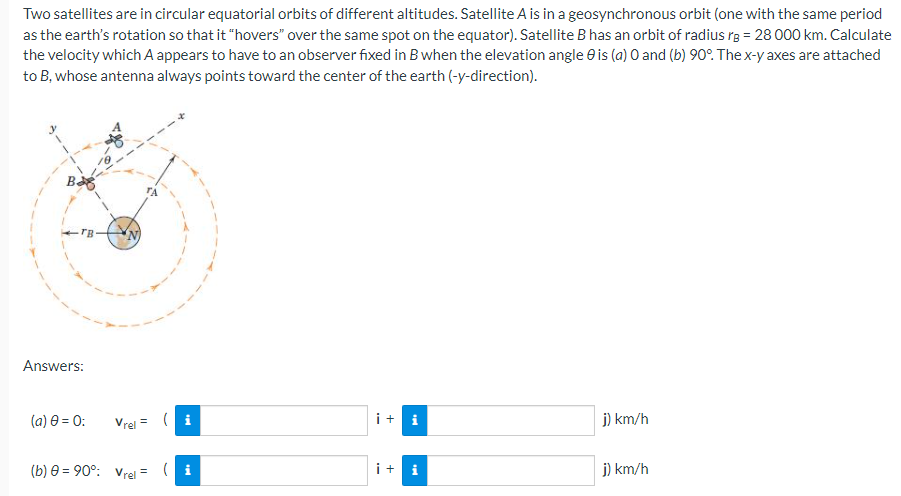
Two satellites are in circular equatorial orbits of different altitudes. Satellite A is in a geosynchronous orbit (one with the same period as the earth's rotation so that it "hovers" over the same spot on the equator). Satellite B has an orbit of radius rB = 28000 km. Calculate the velocity which A appears to have to an observer fixed in B when the elevation angle θ is (a) 0 and (b) 90∘. The x-y axes are attached to B, whose antenna always points toward the center of the earth (-y-direction). Answers: (a) θ = 0: vrel = km/h (b) θ = 90∘: vrel = km/h